Voronoi 图和 Delaunay 三角剖分

发表于 | 分类于 | 阅读次数：

介绍

Voronoi 图的定义

又叫泰森多边形或 Dirichlet 图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。

Voronoi 图的特点

  1. 每个V多边形内有一个生成元
  2. 每个V多边形内点到该生成元距离短于到其它生成元距离
  3. 多边形边界上的点到生成此边界的生成元距离相等
  4. 邻接图形的 Voronoi 多边形界线以原邻接界线作为子集。

Voronoi 图的应用

在计算几何学科中的重要地位，由于其根据点集划分的区域到点的距离最近的特点，其在地理学、气象学、结晶学、航天、核物理学、机器人等领域具有广泛的应用。如在障碍物点集中，规避障碍寻找最佳路径。

算法分析

Voronoi 图有着按距离划分邻近区域的普遍特性，应用范围广。生成V图的方法很多，常见的有分治法、扫描线算法和 Delaunay 三角剖分算法。

建立 Voronoi 图方法和步骤

本次实验采用的是 Delaunay 三角剖分算法。主要是指生成 Voronoi 图时先生成其对偶元 Delaunay 三角网，再找出三角网每一三角形的外接圆圆心，最后连接相邻三角形的外接圆圆心，形成以每一三角形顶点为生成元的多边形网。如下图所示。

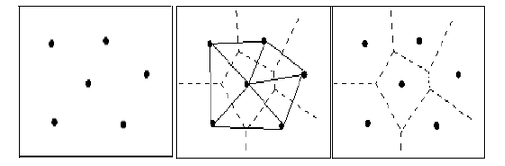
建立 Voronoi 图算法的关键是对离散数据点合理地连成三角网，即构建 Delaunay 三角网。

建立 Voronoi 图的步骤为：

  1. 离散点自动构建三角网，即构建 Delaunay 三角网。对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。
  2. 计算每个三角形的外接圆圆心，并记录之。
  3. 遍历三角形链表，寻找与当前三角形 pTri 三边共边的相邻三角形 TriA，TriB 和 TriC。
  4. 如果找到，则把寻找到的三角形的外心与pTri的外心连接，存入维诺边链表中。如果找不到，则求出最外边的中垂线射线存入维诺边链表中。
  5. 遍历结束，所有维诺边被找到，根据边画出维诺图。

Delaunay 三角网的生成

建立 Voronoi 图的关键是 Delaunay 三角网的生成。Delaunay 三角网的特性：
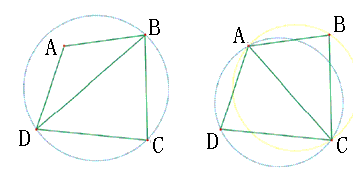
（1）空圆性，任一三角形外接圆内部不包含其他点。
（2）最接近：以最近临的三点形成三角形，且各线段（三角形的边）皆不相交。
（3）唯一性：不论从区域何处开始构建，最终都将得到一致的结果。
（4）最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。
（5）最规则：如果将三角网中的每个三角形的最小角进行升序排列，则 Delaunay 三角网的排列得到的数值最大。
（6）区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。
（7）具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。
Delaunay 剖分是一种三角剖分的标准，实现它有多种算法。本次采用 Bowyer-Watson 算法，算法的基本步骤是：
（1）构造一个超级三角形，包含所有散点，放入三角形链表。
（2）将点集中的散点依次插入，在三角形链表中找出其外接圆包含
插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在 Delaunay 三角形链表中的插入。
（3）根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入 Delaunay 三角形链表。
（4）循环执行上述第 2 步，直到所有散点插入完毕。

关键步骤 2 如下图所示：

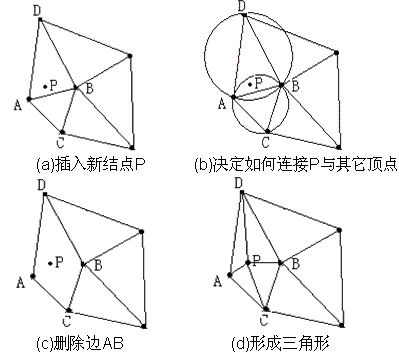
步骤3的局部优化的准则指的是：
1.对新形成的三角形进行优化，将两个具有共同边的三角形合成一个多边形。
2.以最大空圆准则作检查，看其第四个顶点是否在三角形的外接圆之内。
3.如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。

LOP (Local Optimization Procedure) 处理过程如下图所示：

0%