代价函数
逻辑回归:
$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$

不将偏差项正则化:
其中正则项中的 $\Theta_{ji}^{l}$ 当 $i=0$ 时不会进行求和,和之前的逻辑回归中的正则化一样
反向传播算法
目标: $min_{\Theta}J(\Theta)$
Need code to compute:
- $J(\Theta)$
- $\dfrac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)$
梯度下降算法正向传播
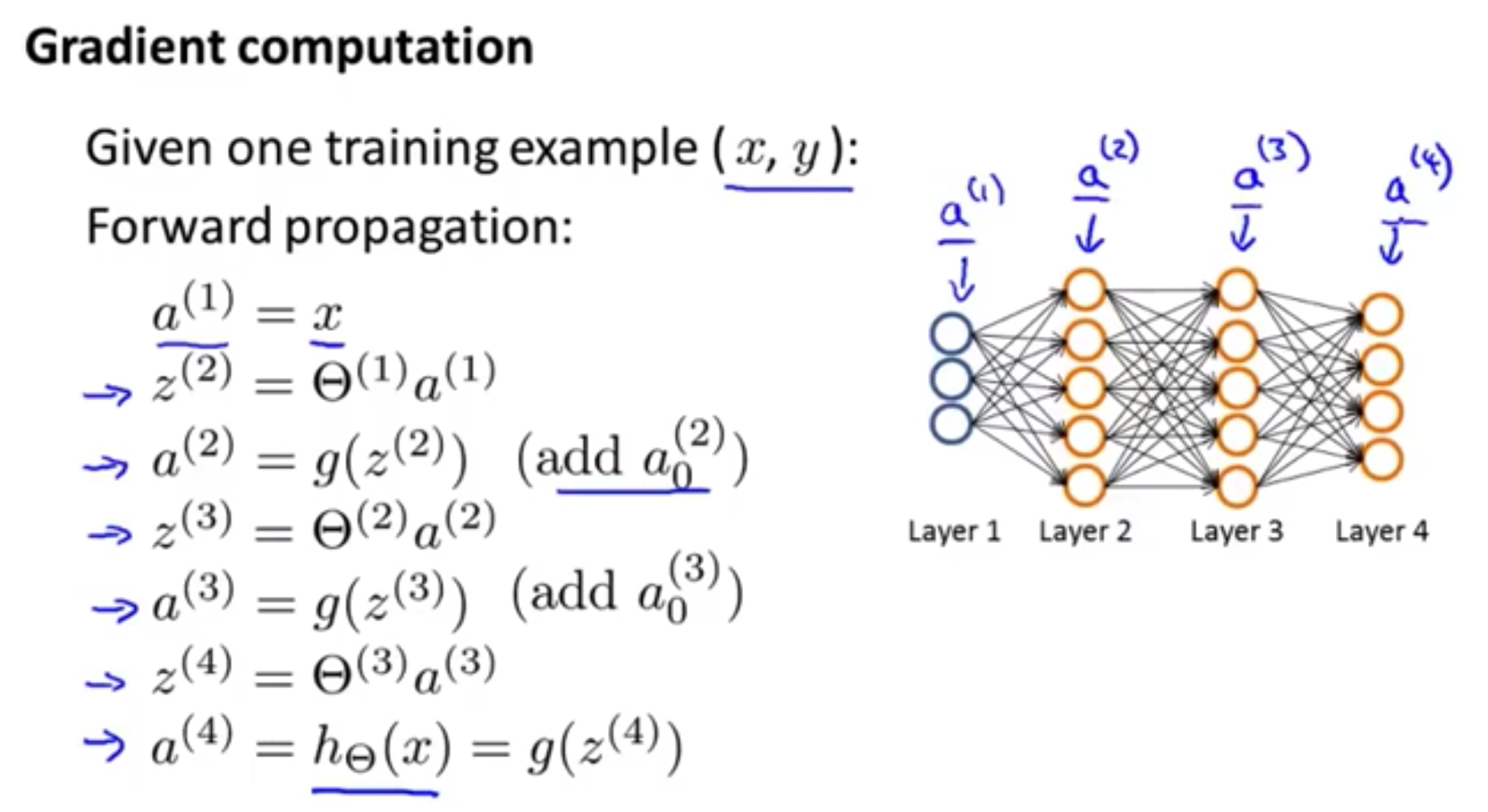
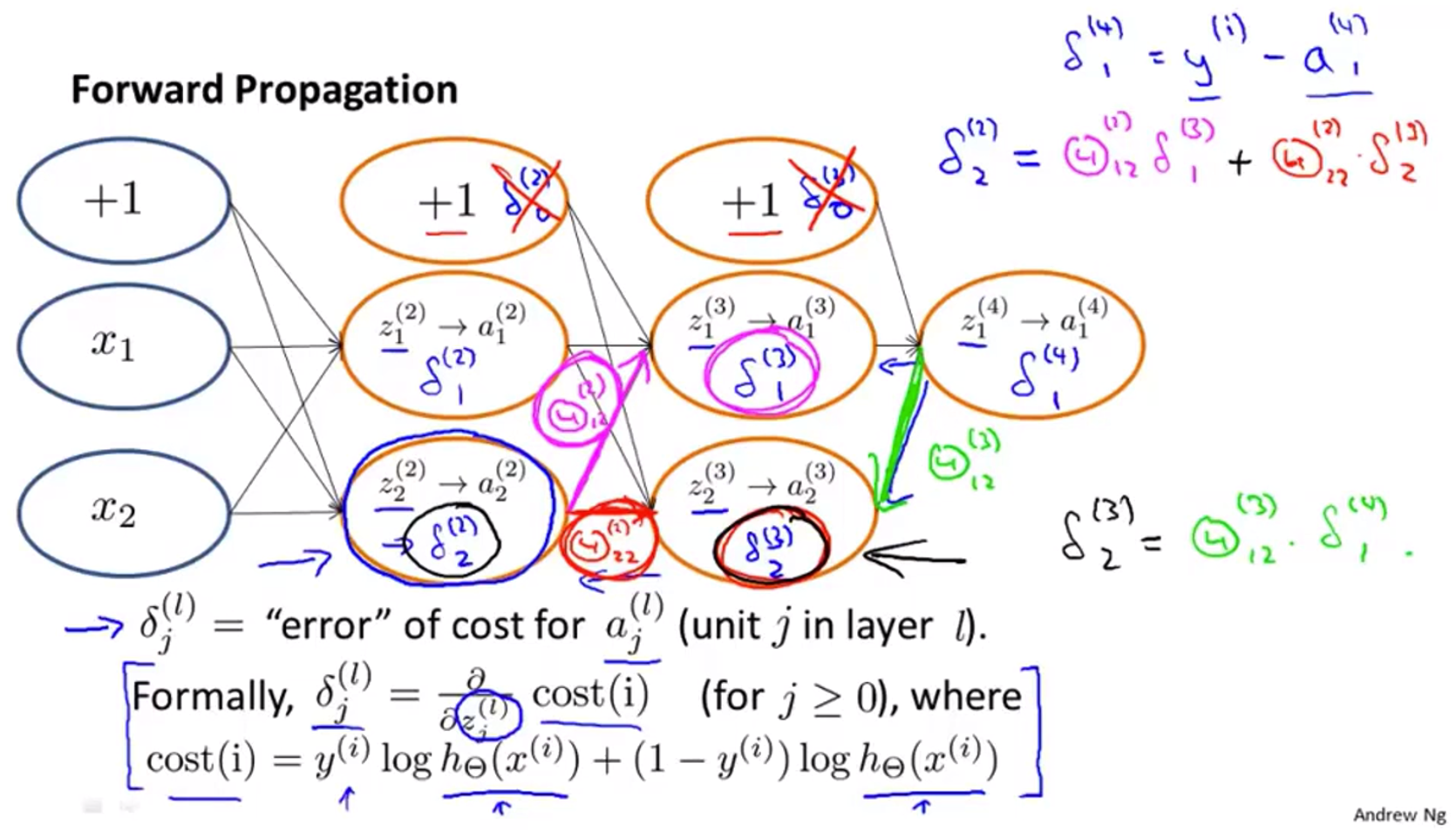
反向传播算法
$\delta_j^{(l)}=$error of node $j$ in layer $l$
For each output unit (layer L = 4):
$\delta_j^{(l)}=\alpha_j^{(4)}-y_j$ 其中 $\alpha_j^{(4)}=(h_{\Theta}(x))_j$

. 就是乘法操作
$g’(z^{(3)})$ 是输入值为 $z^{(3)}$ 时候的所求导数
$a^{(3)}$ 是 *第3层激活向量
没有 $\delta_j^{(1)}$ 因为第一层没有误差
在忽略正则项的情况下可以证明:
$\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_j^{(l)}\delta_j^{(l+1)}$
反向传播算法的实现
Training set $\{(x^{(1)}, y^{(1)}),\cdots ,(x^{(m)}, y^{(m)})\}$
Set $\Delta_{ij}^{(l)}=0$ (for all $l,i,j$) use to compute $\dfrac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)$
For $i=1$ to $m$
Set $a^{(1)}=x^{(i)}$
Perform forword propagation to compute $a^{(l)}$ for $l=2,3,\cdots,L$
Using $y^{(i)}$, compute $\delta^{(L)}=a^{(L)}-y^{(i)}$
Compute $\delta^{(L-1)},\delta^{(L-2)},\cdots,\delta^{(2)}$
$\Delta_{ij}^{(l)}:=\Delta_{ij}^{(l)}+a_j^{(l)}\delta_j^{(l+1)}$ 向量形式:$\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T$
$D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}$ if $j\neq0$
$D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}$ if $j=0$
可以证明 $\dfrac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=D_{ij}^{(l)}$
理解反向传播
梯度检测
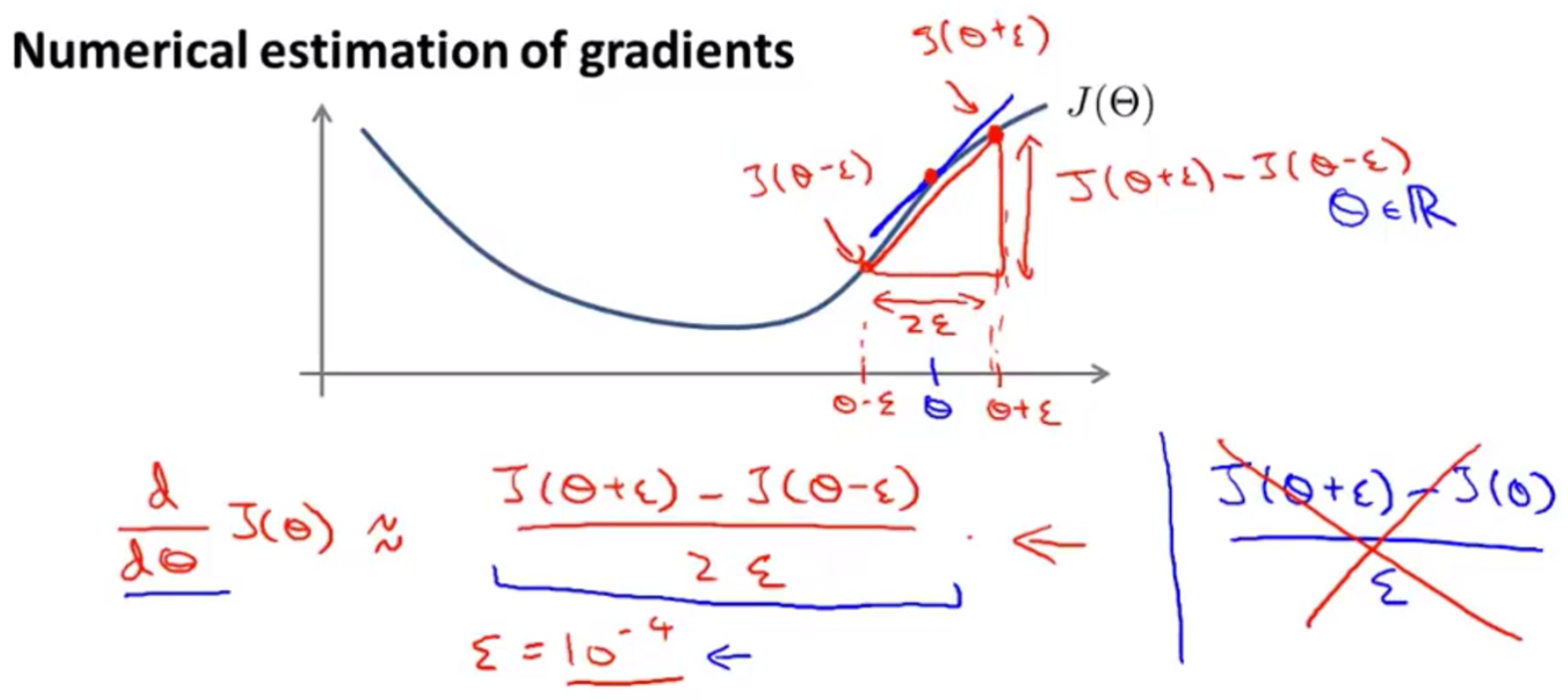


其中DVec是反向传播之中求得的导数
梯度检测的实现:
- 实现反向传播计算DVec(展开 $D^{(1)}$ , $D^{(2)}$ , $D^{(3)}$)
- 实现数值上的梯度检验计算gradApprox
- 确保这以上两个数值有相似的值(只有几位小数的差距)
- 关掉梯度检验,使用反向传播代码(DVec)进行学习(不要使用gradApprox,因为它非常慢)
梯度检测的重要点:
在训练分类器之前一定要确保禁用了梯度检测代码,如果在每一次梯度下降的迭代中都进行梯度检测计算,代码运行会非常缓慢
$\Theta$ 随机初始化
不可以将所有 $\theta$ 值设为0,那样的话进行每次梯度下降以后 $\theta$ 仍旧相等(权重相等),每个单元都一样,相当于只计算一个特征
随机初始化:解决对称权重问题

注: 这里的 $\epsilon$ 和之前梯度检测中的要区分开
