分类 Classfication
$y \in \{1,0\}$
0: “Negative Class”
1: “Positive Class”
逻辑回归
逻辑回归是一种分类方法
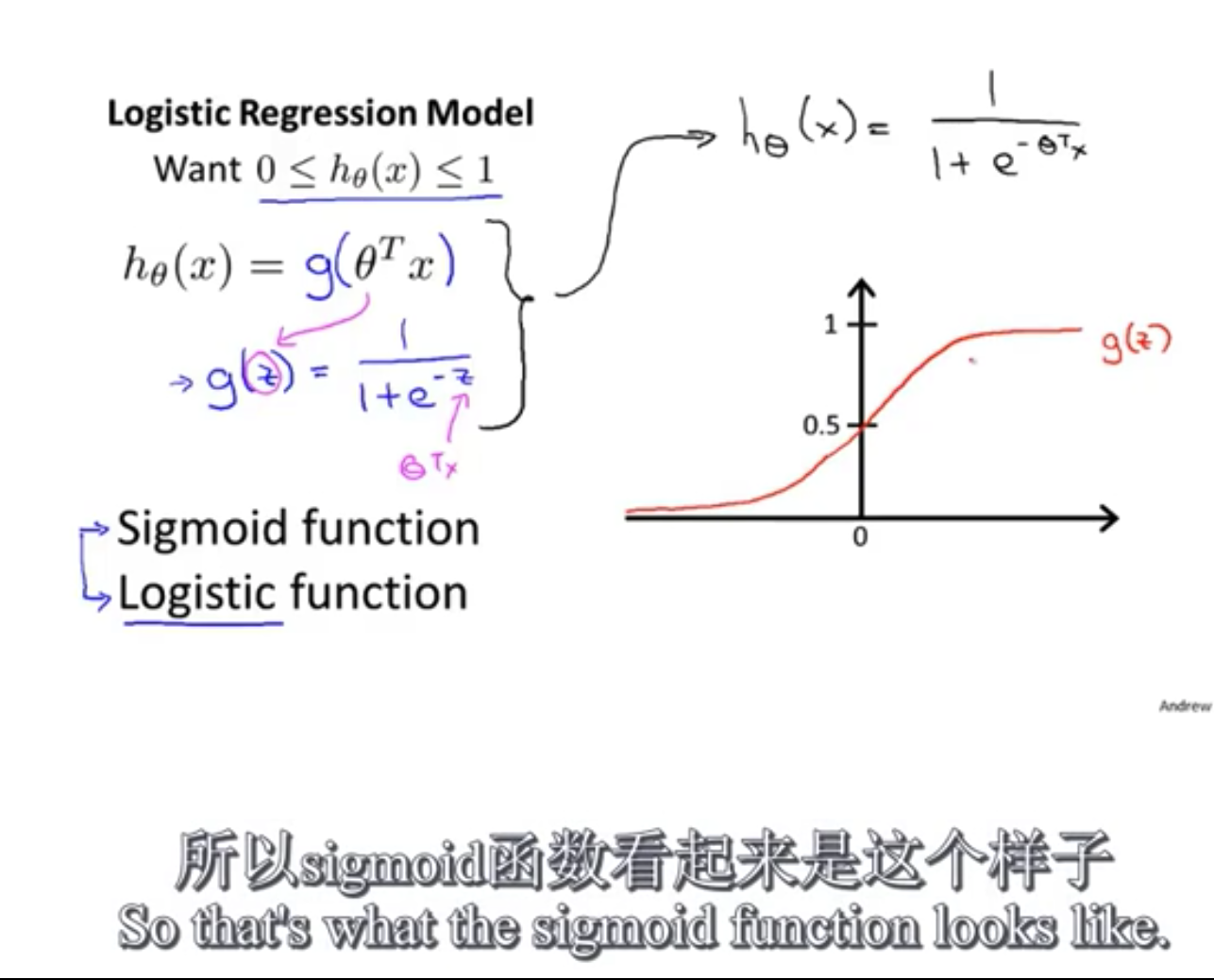
Logistic Regression Model
Want $ 0 \leq h_\theta(x) \leq 1$
$h_\theta(x)=g(\theta^Tx)$
其中 $g(z)=\dfrac{1}{1+e^{-z}}$ ,称作Sigmoid函数或Logistic函数
$h_\theta(x)=P(y=1|x;\theta)$
假设陈述
$y=1$ if $h_\theta(x)\geq 0.5$
$y=0$ if $h_\theta(x) \< 0.5$
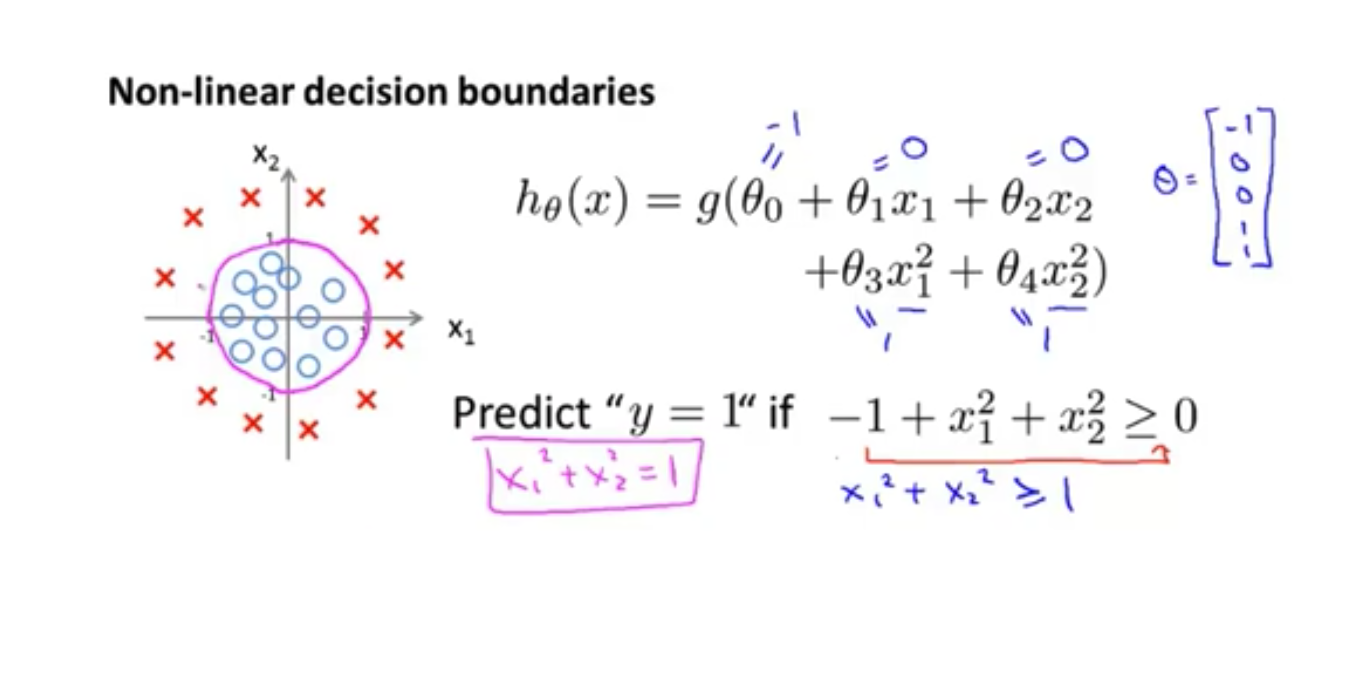
决策界限
Dicision boundary
代价函数
Training set: $\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})\}$
examples:
$x \in\left[\begin{matrix}x_0 \\ x_1 \\ \cdots \\ x_n\end{matrix}\right]$
$x_0=1,y \in \{0,1\}$
$h_\theta(x)=\dfrac{1}{1+e^{\theta^Tx}}$
How to choose parameters $\theta$ ?
Linear regression线性回归中的代价函数:
$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_\theta(x^{(i)}-y^{(i)}))^2=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})$
$Cost(h_\theta(x^{(i)}),y^{(i)})=\frac{1}{2}(h_\theta(x^{(i)}-y^{(i)}))^2$
如果直接用在逻辑回归会造成损失函数是非凸函数(non-convex)
Logistic regression cost function 逻辑回归代价函数

简化代价函数与梯度下降
将上一章的代价函数合并成一个等式( $y=0 \ or \ 1 \ always$ ):
$Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))$
$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})$
$=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]$
(这个代价函数由极大似然法得来)
To fit parameters $\theta$:
$\min_\theta J(\theta)$
To make a prediction given new $x$ :
Output $h_\theta(x)=\dfrac{1}{1+e^{\theta^Tx}}$
运用梯度下降法 Gradient Descent:
Want $\min_\theta J(\theta)$ :
Repeat {
$\theta_j:=\theta_j-\alpha\dfrac{\partial}{\partial\theta_j}J(\theta)$
}
也就是:
Repeat {
$\theta_j:=\theta_j-\alpha\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$
}
这个式子和线性回归的式子一样,但是$h_\theta(x)$不一样
高级优化
Optimization algorithms:
- Gradient descent
- Conjugate gradient 共轭梯度法
- BFGS
- L-BFGS
使用后三种算法时,
优势:
- 不用手动选择 $\alpha$
- 一般来说比梯度下降法更快
劣势:
- 更加复杂
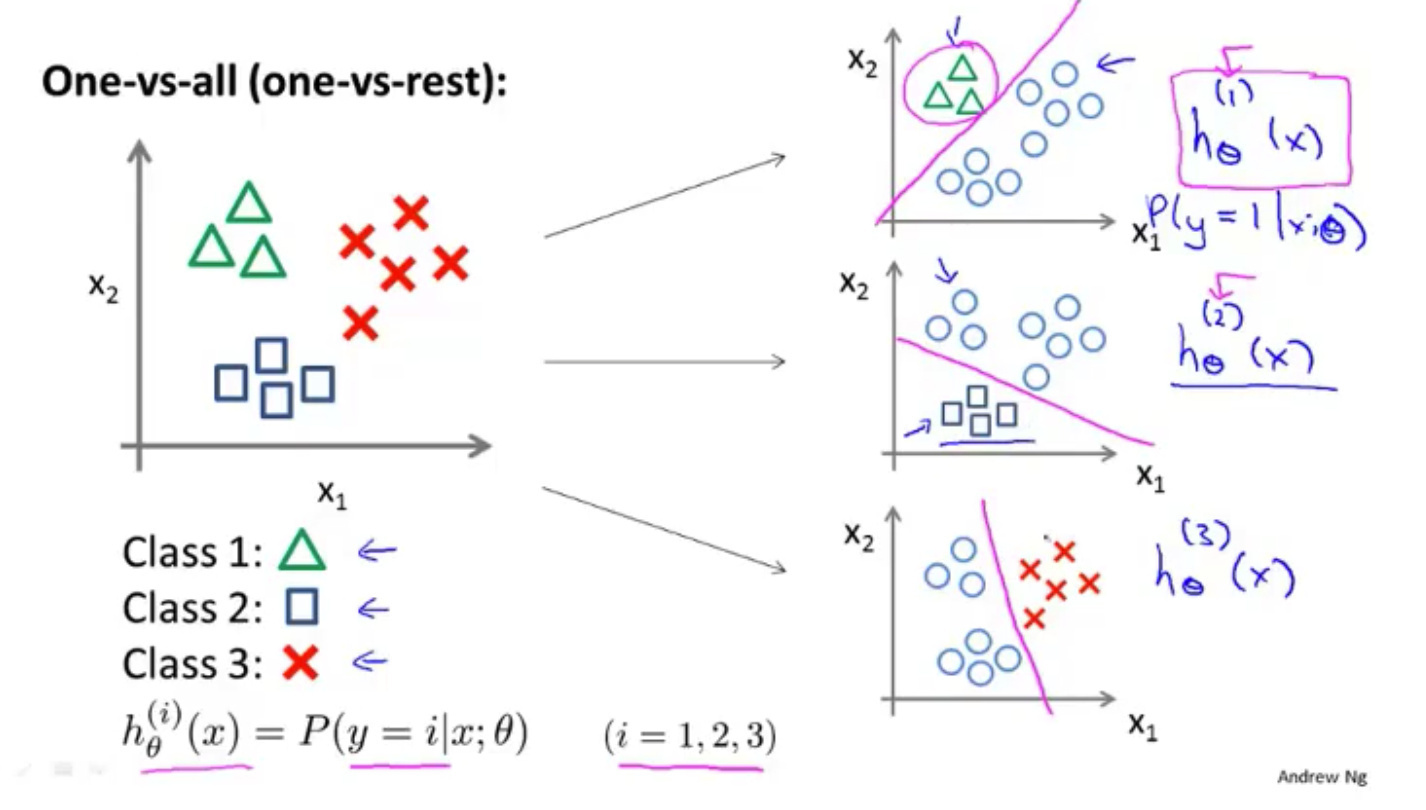
多元分类:一对多